Kind III bursts are normally described as a two-step course of: energetic electrons excite Langmuir waves, that are then transformed into radio emission close to the plasma frequency (Ginzburg & Zhelezniakov 1958). The latest discovery of Basic-Harmonic pairs by Parker Photo voltaic Probe (PSP) exhibits that many basic sort III bursts are weak and composed of quick, quickly various components whose depth rises rapidly after which decays extra slowly at a set frequency (Jebaraj et al. 2023), and PSP observes hundreds of such bursts throughout each shut encounter (Pulupa et al. 2025). This raises a conundrum: why are so many of those bursts noticed, whereas a transparent optimistic velocity-space slope anticipated within the classical bump-on-tail image is uncommon (Lin et al. 1981)? This led us to revisit the linear instability answerable for Langmuir waves.
We concentrate on the entrance of an impulsively ejected energetic electron inhabitants. At a given distance from the supply, sooner electrons arrive first, and slower ones are nonetheless in transit. The mechanism of wave progress as a result of quick electrons arriving and their consequent absorption by slower electrons was first proposed by Zaitsev et al. (1974). Domestically, this manifests as a truncation of the low-velocity facet of the energetic tail of the electron distribution (as proven in left-top panel of Determine 1). This transferring truncation is sufficient to linearly drive Langmuir waves, although the underlying tail wouldn’t create a classical optimistic slope.
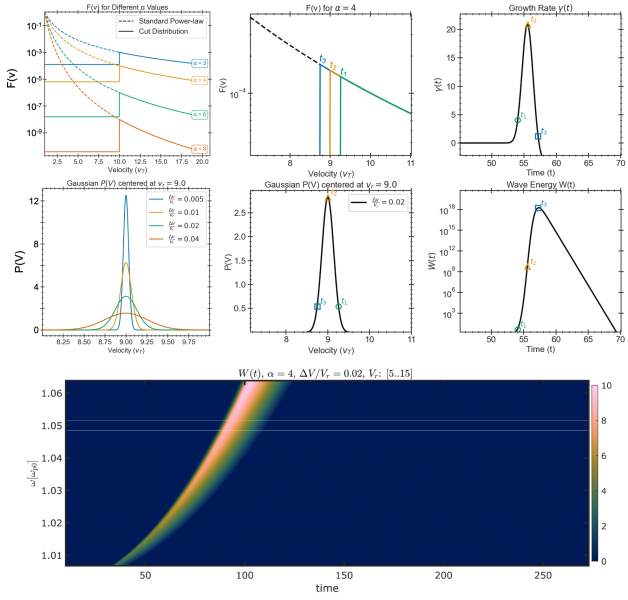
The photo voltaic wind density is randomly inhomogeneous and small density fluctuations refract and sometimes mirror electrostatic waves, so the waves’ part velocity fluctuates alongside their path. Thus, they pattern a slender likelihood distribution of part velocities across the part velocity in homogeneous plasma (Voshchepynets et al. 2015). The middle and width of this distribution encode how fluctuations shift and broaden the efficient wave–particle interplay. When the entrance of the electron inhabitants sweeps throughout this resonant band, wave progress rises quickly; after slower electrons arrive, Landau damping dominates and the waves decay. Scattering of these waves on the identical inhomogeneities converts a part of the power into an electromagnetic wave mode across the basic plasma frequency, so the radio sign largely inherits the identical fast-rise, slower-decay envelope, no less than through the progress and early decay. This sequence at a set location is summarized schematically within the center and proper panels of Determine 1.
The time-of-flight instability
In Krasnoselskikh et al. (2025), we constructed a time-dependent linear mannequin at a set location. We take into account the impulsive injection of an brisk electron tail and account for the time-of-flight truncation at its entrance. The background random density inhomogeneities are described by a likelihood distribution for the wave part velocity. For instinct, we use a slender, almost Gaussian distribution and derive a distribution from Gaussian density statistics that permits for each single and occasional a number of reflections on small density humps. This probabilistic description is the core of the mannequin: the native progress charge is the typical of the native linear increment over the phase-velocity distribution, and the wave power follows from integrating that progress in time. The sequence from the truncated tail, by way of the resonant band, to the ensuing progress charge and wave power is illustrated for a easy Gaussian resonant band in Determine 1.
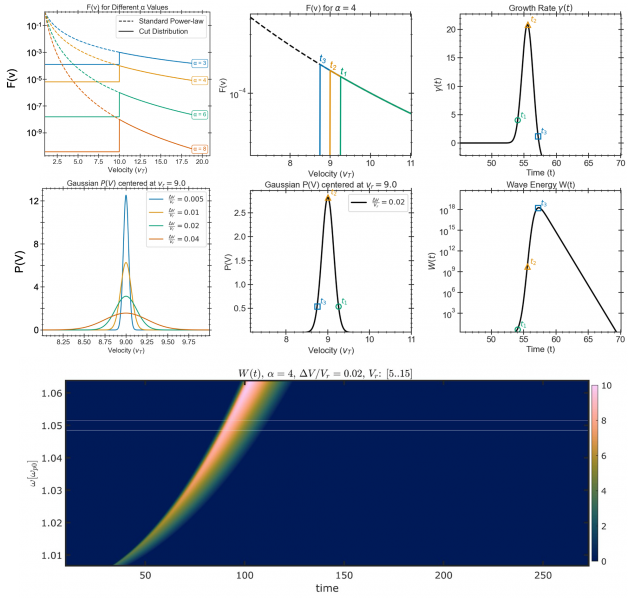
Determine 1. Illustration of the time-dependent instability at a set location (tailored from Krasnoselskikh et al. 2025). High left: energetic-electron distribution $F(V)$ for 4 completely different power-law tails. High center: energy regulation with index $alpha = 4$; vertical-coloured traces mark the truncation on the entrance at three successive occasions $t_1 < t_2 < t_3$. Backside left: Gaussian likelihood distribution $P(V)$ of wave part velocities centered on the resonant velocity $v_r$, with 4 completely different widths and backside center panel exhibits for $Delta V / V_r = 0.02$; symbols present the relative place of the entrance on the identical 3 times. High proper: instantaneous linear progress charge $gamma(t)$, which peaks when the entrance overlaps the middle of the resonant band ($t_2$) and turns into damaging as soon as slower electrons dominate ($t_3$). Backside proper: corresponding wave power $W(t)$, obtained by integrating $gamma(t)$, exhibiting a speedy rise and slower decay; the symbols $t_1$, $t_2$, and $t_3$ are constant throughout all panels. Backside panel exhibits the evolution of Langmuir wave spectrum at some given distance, pushed by an brisk inhabitants of electrons with $alpha = 4$ and $Delta V/V_R = 0.02$. The spectrum consists of waves with resonant velocities (in models of thermal velocity), $V_R = 5-15 V_T$.
We map the outcomes at three consequential moments in time. First, the slope of the energetic tail: a shallower tail gives extra free power close to the truncation and strengthens progress. Second, the resonant part velocity: decrease resonant velocities produce stronger progress and better peaks, whereas increased resonance shifts the motion in time and weakens the height as a result of the entrance should advance additional earlier than it overlaps the resonant band. Third, the fluctuation degree: weaker fluctuations produce a narrower distribution, focus resonance, and provides sharper, bigger peaks; stronger fluctuations broaden the distribution, shift the efficient resonance towards decrease velocities, and scale back and smear out the height. In all instances, the expansion is largest when the entrance pace crosses the resonant band, the rise is speedy because the overlap builds, and the decay is slower as soon as the slower electrons arrive, and damping prevails. After electrostatic-to-electromagnetic conversion on inhomogeneities, this linear evolution reproduces the uneven envelopes noticed within the basic part. The harmonic stays in keeping with normal nonlinear coupling of major and backscattered Langmuir-like modes and isn’t thought of right here.
Why this issues
By shifting consideration from a beam with a optimistic slope to the truncated entrance of ejected electrons interacting with a fluctuation-broadened resonance, we get hold of a easy, linear, and observation-aligned set off for the basic part of Kind III bursts. This framework explains the prevalent fast-rise and slower-decay envelopes, is in keeping with the shortage of clear beam signatures in particle information taken on the identical occasions and clarifies why fundamentals measured near the Solar could be weak or fade by 1 au. It additionally hyperlinks measurable burst morphology to ambient fluctuation ranges and to the efficient resonance of Langmuir waves, offering concrete assessments for future PSP and Photo voltaic Orbiter observations. The mannequin is deliberately linear and most applicable for weaker occasions; it establishes a transparent baseline on prime of which nonlinear saturation and suggestions could be added.
References
Ginzburg, V. L., & Zhelezniakov, V. V. 1958, Sov. Astron., 2, 653.
Jebaraj, I. C., Krasnoselskikh, V., Pulupa, M., Magdalenic, J., & Bale, S. D. 2023, ApJL, 955, L20.
Krasnoselskikh, V., Jebaraj, I. C., Cooper, T. R. F., et al. 2025, ApJ, 990, 100.
Lin, R. P., Potter, D. W., Gurnett, D. A., & Scarf, F. L. 1981, ApJ, 251, 364.
Pulupa, M., Bale, S. D., Jebaraj, I. C., Romeo, O., & Krucker, S. 2025, ApJL, 987, L34.
Voshchepynets, A., Krasnoselskikh, V., Artemyev, A., & Volokitin, A. 2015, ApJ, 807, 38.
Zaitsev, V. V., Kunilov, M. V., Mityakov, N. A., & Rapoport, V. O. 1974, Sov. Astron., 18, 147.